Singly Linked List - K-th Node from End
Problem: Get the Kth node from end of a linked list. It counts from 1 here, so the 1st node from end is the tail of list.
For instance, given a linked list with 6 nodes, whose value are 1, 2, 3, 4, 5, 6, its 3rd node from end is the node with value 4.
A node in the list is defined as:
struct ListNode
{
int m_nValue;
ListNode* m_pNext;
};
Analysis: In a list with n nodes, its kth node from end should be the (n-k+1)th node from its head. Therefore, if we know the number of nodes n in a list, we can get the required node with n-k+1 steps from its head. How to get the number n? It is easy if we scan the whole list from beginning to end.
The solution above needs to scan a list twice: We get the total number of nodes with the first scan, and reach the kth node from end with the second scan. Unfortunately, interviewers usually expect a solution which only scans a list once.
We have a better solution to get the kth node from end with two pointers. Firstly we move a pointer (denoted as P1) k-1 steps beginning from the head of a list. And then we move another pointer (denoted as P2) beginning from the head, and continue moving the P1 forward at same speed. Since the distance of these two pointers is always k-1, P2 reaches the kth node from end when P1 reaches the tail of a list. It scans a list only once, and it is more efficient than the previous solution.
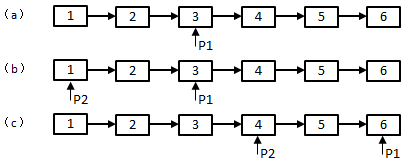
Figure 1: Get the 3rd node from end of a list with 6 nodes
It simulates the process to get the 3rd node from end of a list with 6 nodes in Figure 1. We firstly move P1 2 steps (2=3-1) to reach the 3rd node (Figure 1-a). Then P2 points to the head of a list (Figure 1-b). We move two pointers at the same speed, when the P1 reaches the tail, what P2 points is the 3rd node from end (Figure 1-c).
The sample code of the solutions with two pointers is shown below:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k)
{
if(pListHead == NULL || k == 0)
return NULL;
ListNode *pAhead = pListHead;
ListNode *pBehind = NULL;
for(unsigned int i = 0; i < k - 1; ++ i)
{
if(pAhead->m_pNext != NULL)
pAhead = pAhead->m_pNext;
else
{
return NULL;
}
}
pBehind = pListHead;
while(pAhead->m_pNext != NULL)
{
pAhead = pAhead->m_pNext;
pBehind = pBehind->m_pNext;
}
return pBehind;
}The discussion about this problem is included in my book